Quantization Method In Approximate Nearest Neighbor Search

对于一个检索任务：给定一个query $q \in R^D$，需要在数据集 $X \in R^{N \times D}$ 中找到距离 $q$ 最近的样本，距离度量函数 $d$ 一般使用欧式距离。

$$NN(q) = \arg \min\limits_{x \in X} d(q, x) \tag {1}$$

想要解决这个问题，最朴素的办法是使用 Exact Search，穷举 $q$ 到 $N$ 个样本点之间的距离，这样一定能准确地找到离 $q$ 最近的样本。但由于 Exact Search 的复杂度是 $O(ND)$，空间复杂度 $O(ND)$，而实际的应用场景中往往需要在毫秒级的响应时间同时对存储空间也有要求，数据规模稍大（million）的情况下便无法应用上。

ANN主要思想是通过损失一部分检索精度来最大限度地换取检索速度的提升。目前主流的方法都是试图构建一种特殊的数据索引结构，大致可分为以下4类+用于辅助的索引结构方法：

1. Tree: KD-Tree等；
2. Hash: LSH, ITQ等；
3. Quantization: PQ, OPQ, LSQ++等；
4. Graph: HNSW, NSG等;
5. auxiliary：IMI等。

其中Tree、Hash和Quantization Based的方法一般是基于空间划分的思想，将空间划分成cell/Voronoi，然后利用上某些辅助的索引结构，可以在检索的过程中起到同时降低 $N$ 和 $D$ 来减少检索复杂度，如IVFPQ(PQ + Inverted Index)。

Graph Based的方法一般需要构建 $K$ 近邻图，比起其他方法更占空间资源，但是检索精度一般更高。

trade-off: recall, speed, memory.

Quantization Method：A Brief Story

量化的目的就是减小原始空间的势(cardinality)。

假定样本集 $X = [x_1, x_2,…,x_n] \in R^{d \times n}$ ，量化则试图找到一个quantizer(一种变换)将样本从 $R^{d \times n}$ 映射到一个有限的集合 $C = [c_1, c_2, … c_k]\in R^{d \times k}$ 中，映射之后的样本 $x_i$ 则可以用集合 $C$ 中的某一元素 $c_j$ 表示，同时我们希望 $x_i$ 和 $c_j$ 的距离尽可能小。其中集合$C$ 也叫codebook ， $C$ 中每一个元素称为codeword。

量化的过程可以看作是由一个编码器 $p$ 和解码器 $q$ 两个函数来表示。在给定$C$ 的前提下，$p$ 将样本编码成一个index，$q$ 则根据 $p$ 产生的index从 $C$ 中找出 index 对应的 codeword 。

下面主要叙述近年来比较经典的量化方法，它们都可以看成是在优化同一个目标函数，只是不同的方法对应有不同的约束。

Vector Quantization(VQ)

作为最经典的量化方法，VQ使用MSE来衡量量化效果：

$$\min\limits_{C}\sum\limits_{i=1}^{N}\| x_i - q(p(x_i))\|_2^2​\tag {2} \label{eq: eq2}$$

当给定 codebook $C$ 时，上式满足 Lloyd’s condition: $p(x_i)$ 必须将 $x_i$ 映射到 $C$ 中离它最近的codeword 的 index。Lloyd’s condition不论当 codebook 是什么形式都必须被满足。上式等价于K-means，求解 $C$ 的过程也和K-means一样。其中$p(x) \in \{1, 2,…, k\}$ , 故原式也可以写成：

$$\min\limits_{C, G \in Ind}\left\| X-CG \right\|_F^2 \tag {3}$$

此时，$C$ 表示 $k$ 个聚类中心，$G=[g_1, g_2,…, g_n] \in \{0, 1\}^{k \times n}$ 是Indicator Matrix，$g_i$ 只有第 $j$ 个元素为1，表示第 $i$ 个样本隶属第 $j$ 个聚类中心。

由于我们将 $n$ 个样本映射成 $k$ 个codeword，于是我们也能知道每一个样本点所隶属的codeword。那么在检索阶段，query到每个样本点之间的距离，只需要通过计算query到这 $k$ 个codeword之间的距离得到一个长度为$k$ 的lookup table。假设样本点 $x_i$ 隶属于第 $j$ 个codeword，然后query到 $x_i$ 的距离就可以通过查找表的第 $j$ 个值来近似。

训练过程等同于K-means，时间复杂度为 $O(ndk)$ ，空间复杂度为 $O((n+k)d)$ 。检索时计算query到 $n$ 个样本距离的空间复杂度为 $O(kd)$ ，时间复杂度为 $O(n+kd)$ 。为了避免于exact search，我们可以建立一个inverted file structure $Z$，$Z$ 可以看作是一个dictionary，有 $k$ 个 key，第 $j$ 个key对应的value表示所有隶属于第$j$ 个codeword的样本的index组成的List。 那么当我们使用VQ来进行检索时，首先query只需要跟 $k$ 个codeword计算距离，假设找到离最近的codeword是 $c_j$ ，那么只需要在 $Z[j]$ 中的样本里头进行exact search 找到最近邻。

通过实验发现，VQ一般具有如下性质：

1.目标函数值越小，检索效果会越好；所以可以通过降低目标函数值来提升检索效果。

2.$k$ 值越大，目标函数值会越小。所以可以通过增大 $k$ 来提升检索效果。

我们可以想象，当$k$一直增大到$n$时，此时每个样本单独成一类，此时的VQ就等价Exact Search，recall能达到最好，但是却不适用。实际使用中由于存储设备和检索时间的约束，$k$ 值一般不会取得特别大。

Product Quantization(PQ)

2012年，Hervé Jégou等人提出了PQ，其主要思想是将原始 $d$ 维样本空间等长度切分为 $m$ 个正交的子空间，每个子空间的维度是 $\frac{d}{m}$, 由此在ANN领域中开辟了新的方向，吸引了很多学者的关注。 PQ问题可以表述成下式：

$$\min\limits_{C_1, C_2, ..., C_m}\sum\limits_{i=1}^{N}\| x_i - q(p(x_i))\|_2^2​\tag {4} \label{eq: eq4}$$ $$s.t. q \in C = C_1 \times C_2 \times ... \times C_m​$$

$C_j$ 表示第 $j$ 个子空间的codebook，式 $\eqref{eq: eq4} $ 在式 $\eqref{eq: eq2} $ 的基础上对codebook加上了约束，使得此时的codebook $C$ 由每一个子空间的codebook的笛卡儿积构成。这么做最大的好处就是在与K-means在使用相同的codebook存储容量的情况下，能表示更多的codeword。假设聚类个数 $k$ 取256，PQ的每一个codebook 有256个codeword ,当 $m$ 取4，此时那么PQ方法能表示的codeword的总数是 $256^4$ ，远多于 k-means 所能表示的256个。

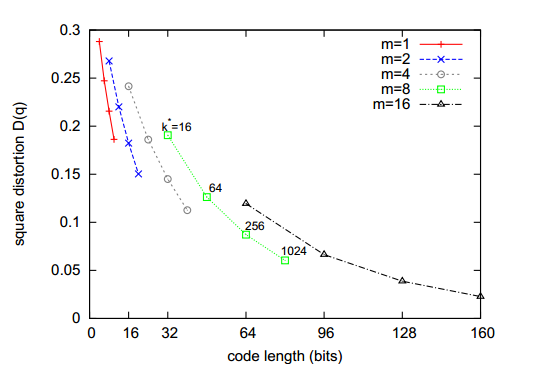
该问题的优化过程等价于对 $m$ 个子空间分别进行K-means。

检索时的时间复杂度为 $O(kd+nm)$ ，空间复杂度为 $O(kd+nm)$ 。

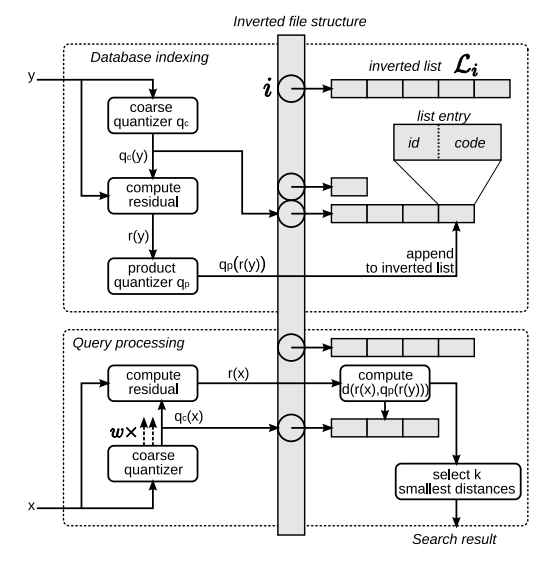
为了进一步加快检索过程，作者在PQ的基础上加上了基于k-means的Inverted file structure, 第 $i$ 个 inverted list 存储的是隶属第 $i$ 类样本的id和样本到聚类中心的残差经过PQ编码之后的code。此时的k-means 可以被看作是粗过滤，目的是减少query所需遍历的样本个数。

Optimized Product Quantization(OPQ)

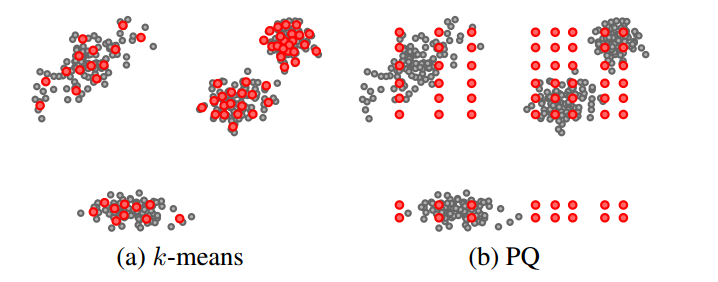
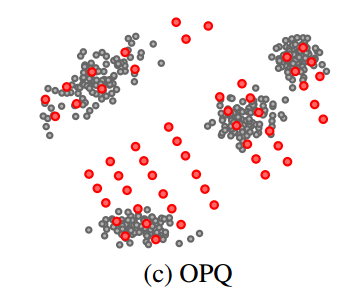
前面已经说到，使用k-means 时增大 $k$ 对量化误差最小化是有好处的，但是实际中往往受限于内存和时间。而且$k$ 过大训练阶段的开销也成问题，所以实际中并不常用。PQ能够很好的增大 $k$ 来减小量化误差，如上图 $(b)$ 所示，在每个子空间只聚了8个类。仔细观察我们可以发现， $(b)$ 中的样本点并没有很好的“附着“在 codeword 上，如果此时对数据/样本点做一个旋转变化，可以使更多中心附着在样本上，使得目标函数值进一步减小，如 $(c)$ 。

在PQ的基础上，寻找一个最优的旋转矩阵 $R$ 使量化误差最小，可以表述成如下优化问题：

$$\min\limits_{R, C_1, ..., C_M} \sum\limits_{i=1}^N\| x_i - q(p(x_i)) \|_2^2 \tag{5}$$ $$s.t. q\in C = \{Rc^{'} | c^{'} \in C_1\times C_2 \times ... \times C_M, R^TR=I \}$$

该问题可以使用交替优化的方式求解：

1.Fix $R$：原问题 $(5)$ 等价于PQ问题；

2.Fix $C_1, C_2,…,C_M$：令 $Y=[y_1, y_2,…y_N]$ ，$y_i$ 对应 $x_i$ 隶属的codeword , $(5)$等价于

$$\min\limits_R \| X-RY \|_F^2$$

该问题是一个典型的Orthogonal Procrustes Problem，

$$\begin{align} R & =\arg \min\limits_R \| RY-X \|_F^2 \\ & =\arg \min \|Y\|_F^2 + \|X\|_F^2 - 2<RY, X> \\ & = \arg \max <R, XY^T> \\ & = \arg \max <R, U\Sigma V^T> \\ & = \arg \max <U^TRV, \Sigma> \\ \end{align}$$

由于$U^TRV$ 是正交矩阵，所以$I = U^TRV$ , $R = UV^T$ .

Locally optimized product quantization(LOPQ)

在IVFPQ的基础上，对inverted file structure中每一个inverted list中的残差向量进行OPQ。

Non-orthogonal Multi-Codebook Quantization(MCQ)

前面基于PQ的方法都是假设样本具有 $M$ 个相互正交的属性组，然后在这 $M$ 个属性组中进行 k-means 产生 $M$ 个正交的 codebook，于是每一个向量 $x$ 都可以由分别从这 $M$ 个codebook中选取的一个codeword进行拼接后的向量来表示。在实际中，数据的每一个属性往往都不是正交的，所以实际中量化的效果还是有进一步的的提升空间。如下图PQ code所示。

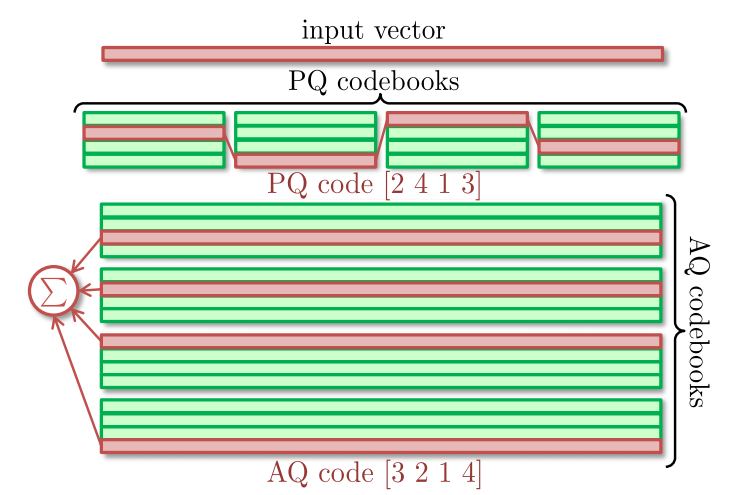
最近的工作更多关注于使用 $M$ 个非正交的codebook对向量进行表示，每一个向量 $x$ 都可以由分别从这 $M$ 个codebook 中选取的一个codeword 相加后的向量来表示。如上图AQ code所示。这样做就没有了正交的假设，此时 codeword 的表示能力也就越强。但是带来的副作用是计算开销的增大，具体来说这些 Non-orthogonal MCQ 方法都是在解如下这个问题：

$$\min\limits_{C_1, ..., C_M} \sum\limits_{i=1}^N\| x_i - q(p(x_i)) \|_2^2 \tag {6}$$ $$s.t. q \in C = \{c | c = \sum\limits_{j=1}^M c_{jk_j} \}$$

等价于

$$\min\limits_{C} \sum\limits_{i=1}^N\| x_i - \sum\limits_{j=1}^M c_{jk_j}\|_2^2 \tag{7}$$

$c_{jk_j}$ 表示第 $j$ 个codebook中的第 $k_j$ 个codeword。假设第 $j$ 个codebook $C_j$ 划分成 $m$ 等分，第 $z$ 份用 $C_{jz}$ 表示。那么如果给上式加上约束使得 $C_j$ 中除了 $C_{jj}$ ，其余部分的值都为0，则上式与PQ等价。这说明PQ方法是上式的一种特例。

假设某一样本点 $x$ 对应的 codeword 是 $\sum\limits_{j=1}^M c_{jk_j}$, 那么在检索阶段，query $q$ 到样本 $x$ 的距离为

$$\| q - \sum\limits_{j=1}^M c_{jk_j} \|_2^2 = \| q \|_2^2 - 2\sum\limits_{j=1}^M q^Tc_{jk_j} +\sum\limits_{j_1=1}^M \sum\limits_{j_2=1}^M c_{j_1k_{j_1}}^T c_{j_2k_{j_2}}$$

其中第1项是常量，第二项可以和之前PQ的方法类似可以构建一张 lookup table ，关键是第三项的计算。根据第三项的不同，衍生出了PQ, AQ和，LSQ，LSQ++等一系列新的算法，目的就是为了加速计算。

参考文献

[1] T. Ge, K. He, Q. Ke, and J. Sun, “Optimized product quantization,” IEEE transactions on pattern analysis and machine intelligence(TPAMI), vol. 36, no. 4, pp. 744-755, 2013.

[2] Y. Kalantidis, Y. Avrithis, “Locally optimized product quantization for approximate nearest neighbor search,” in IEEE Conference on Computer Vision and Pattern Recognition(CVPR), 2014, pp. 2321-2328.

[3] J. Martinez, S. Zakhmi, H. H. Hoos, and J. J. Little, “LSQ++: Lower running time and higher recall in multi-codebook quantization,” in IEEE Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 491-506.